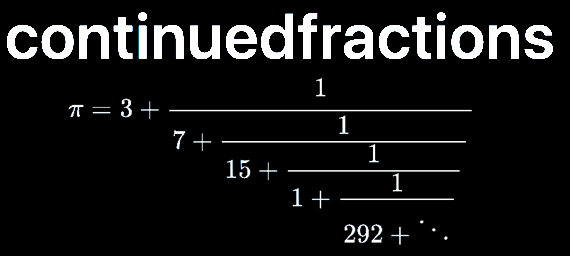
continuedfractions.continuedfraction#
- class continuedfractions.continuedfraction.ContinuedFraction(*args: Any, **kwargs: Any)[source]#
An object-oriented representation of a (finite) simple continued fraction.
An implementation of simple continued fractions as Python objects and instances of the standard library
fractions.Fractionclass, with various properties for the continued fraction, including its elements (or coefficients), the order, convergents, and remainders.The term “simple continued fraction” denotes a specific type of continued fraction where the fractional terms only have numerators of \(1\).
Examples
Construct the continued fraction for the rational 649/200.
>>> cf = ContinuedFraction(649, 200) >>> cf ContinuedFraction(649, 200) >>> cf.as_float() 3.245
Inspect the elements, order, convergents, and remainders.
>>> cf.elements (3, 4, 12, 4) >>> cf.order 3 >>> cf.convergent(0), cf.convergent(1), cf.convergent(2), cf.convergent(3) (ContinuedFraction(3, 1), ContinuedFraction(13, 4), ContinuedFraction(159, 49), ContinuedFraction(649, 200)) >>> cf.remainder(0), cf.remainder(1), cf.remainder(2), cf.remainder(3) (ContinuedFraction(649, 200), ContinuedFraction(200, 49), ContinuedFraction(49, 4), ContinuedFraction(4, 1))
Check some properties of the convergents and remainders.
>>> assert cf.remainder(1) == 1 / (cf - cf.convergent(0))
Construct continued fractions from element sequences.
>>> cf_inverse = ContinuedFraction.from_elements(0, 3, 4, 12, 4) >>> cf_inverse ContinuedFraction(200, 649) >>> assert cf_inverse == 1/cf >>> assert cf * cf_inverse == 1 >>> cf_negative_inverse = ContinuedFraction.from_elements(-1, 1, 2, 4, 12, 4) >>> cf_negative_inverse ContinuedFraction(-200, 649) >>> assert cf_negative_inverse == -1/cf >>> assert cf * cf_negative_inverse == -1
Attributes
An immutable dict of all \(k\)-order convergents of the continued fraction, keyed by order.
The sequence of elements of the continued fraction.
An immutable dict of all even-order convergents of the continued fraction, keyed by order.
The Khinchin mean of the continued fraction, which is defined as the geometric mean of all its elements after the 1st.
An immutable dict of all odd-order convergents of the continued fraction, keyed by order.
The order of the continued fraction, which is the number of its elements minus \(1\).
An immutable dict of all \(k\)-th remainders of the continued fraction, keyed by order.
Methods
Returns the
decimal.Decimalvalue of the continued fraction.as_float()Returns the
floatvalue of the continued fraction.convergent(k, /)Returns the \(k\)-th (simple) convergent of the continued fraction.
from_elements(*elements)Returns a
ContinuedFractioninstance from a sequence of (integer) elements of a (finite) simple continued fraction.left_mediant(other, /, *[, k])Returns the \(k\)-th left-mediant of the continued fraction with another rational number.
remainder(k, /)Returns the \(k\)-th remainder of the continued fraction.
right_mediant(other, /, *[, k])Returns the \(k\)-th right-mediant of the continued fraction with another rational number.
- static __new__(cls, *args: Any, **kwargs: Any) ContinuedFraction[source]#
Creates, initialises and returns instances of this class.
Arguments can be any which are valid for creating objects of the
fractions.Fractionsuperclass.For clarification, valid arguments can be one of the following:
a single instance of
numbers.Rational, includingint,fractions.FractionorContinuedFraction, named or unnameda pair of
numbers.Rationalinstances, includingint,fractions.FractionandContinuedFraction, named or unnameda single
floatordecimal.Decimalvalue that is not a special value such asmath.nan,float('inf'), orDecimal('infinity')a single numeric valid string (
str) - validity is determined in the superclass by thefractions._RATIONAL_FORMATtest
- Returns:
- ContinuedFraction
A full instance of
ContinuedFraction.
Examples
Several example are given below of constructing the simple continued fraction for the number \(\frac{-649}{200}\) in different ways.
>>> ContinuedFraction(-649, 200) ContinuedFraction(-649, 200) >>> ContinuedFraction('-3.245') ContinuedFraction(-649, 200) >>> ContinuedFraction(Decimal('-3.245')) ContinuedFraction(-649, 200) >>> ContinuedFraction('-649/200') ContinuedFraction(-649, 200) >>> ContinuedFraction(Fraction(-649, 200)) ContinuedFraction(-649, 200) >>> ContinuedFraction(ContinuedFraction(649, -200)) ContinuedFraction(-649, 200) >>> ContinuedFraction(Fraction(-649), 200) ContinuedFraction(-649, 200) >>> ContinuedFraction(649, Fraction(-200)) ContinuedFraction(-649, 200) >>> ContinuedFraction(Fraction(-649), ContinuedFraction(200)) ContinuedFraction(-649, 200)
In each of the examples above, the minus sign can be removed from the arguments to the
numbers.Rationalinstance and instead attached to the outer class, e.g.:>>> -ContinuedFraction(649, 200) ContinuedFraction(-649, 200) >>> -ContinuedFraction('3.245') ContinuedFraction(-649, 200) >>> -ContinuedFraction('649/200') ContinuedFraction(-649, 200)
Invalid arguments will raise errors in the
fractions.Fractionsuperclass.
- classmethod from_elements(*elements: int) ContinuedFraction[source]#
Returns a
ContinuedFractioninstance from a sequence of (integer) elements of a (finite) simple continued fraction.Invalid elements will trigger a
ValueError.- Parameters:
- *elementsint
An ordered sequence of integer elements of a (finite) simple continued fraction.
- Returns:
- ContinuedFraction
A new and fully initialised instance of
ContinuedFractionwith the given element sequence.
- Raises:
- ValueError
If any elements are not integers, or any elements after the 1st are not positive.
Examples
Constructing a continued fraction for the rational \(\frac{649}{200}\) using the element sequence \(3, 4, 12, 4\).
>>> c1 = ContinuedFraction.from_elements(3, 4, 12, 4) >>> c1 ContinuedFraction(649, 200)
Constructing the continued fraction of the (multiplicative) inverse \(\frac{200}{649}\) using the element sequence \(0, 3, 4, 12, 4\).
>>> c2 = ContinuedFraction.from_elements(0, 3, 4, 12, 4) >>> c2 ContinuedFraction(200, 649)
Validation for elements containing non-integers or negative integers.
>>> ContinuedFraction.from_elements('0', 1) Traceback (most recent call last): ... ValueError: Continued fraction elements must be integers, and all elements after the 1st must be positive >>> ContinuedFraction.from_elements(0, 1, 2.5) Traceback (most recent call last): ... ValueError: Continued fraction elements must be integers, and all elements after the 1st must be positive >>> ContinuedFraction.from_elements(1, 0) Traceback (most recent call last): ... ValueError: Continued fraction elements must be integers, and all elements after the 1st must be positive >>> ContinuedFraction.from_elements(1, -1) Traceback (most recent call last): ... ValueError: Continued fraction elements must be integers, and all elements after the 1st must be positive
- __neg__() ContinuedFraction[source]#
Division-free negation for a finite simple continued fraction, as described documentation.
The basic algorithm can be described as follows: if \([a_0; a_1,\ldots, a_n]\) is the simple continued fraction of a positive rational number \(\frac{a}{b}\) of finite order \(n\) then \(-\frac{a}{b}\) has the simple continued fraction:
\[\begin{split}\begin{cases} [-a_0;] \hskip{3em} & n = 0 \\ [-(a_0 + 1); 2] \hskip{3em} & n = 1 \text{ and } a_1 = 2 \\ [-(a_0 + 1); a_2 + 1, a_3,\ldots, a_n] \hskip{3em} & n \geq 2 \text{ and } a_1 = 1 \\ [-(a_0 + 1); 1, a_1 - 1, a_2, \ldots,a_n] \hskip{3em} & n \geq 2 \text{ and } a_1 \geq 2 \end{cases}\end{split}\]In applying this algorithm there is an assumption that the last element \(a_n > 1\), as any simple continued fraction of type \([a_0; a_1,\ldots, a_{n} = 1]\) can be reduced to the simple continued fraction \([a_0; a_1,\ldots, a_{n - 1} + 1]\).
- as_float() float[source]#
Returns the
floatvalue of the continued fraction.- Returns:
- float
The
floatvalue of the continued fraction.
Examples
Note that the default
decimalcontext precision of \(28\) is used in these examples.>>> import math >>> math.pi 3.141592653589793
Now construct a
ContinuedFractioninstance from it, and check thefloatvalue.>>> cf = ContinuedFraction(math.pi) >>> cf ContinuedFraction(884279719003555, 281474976710656) >>> cf.as_float() 3.141592653589793
- as_decimal() Decimal[source]#
Returns the
decimal.Decimalvalue of the continued fraction.- Returns:
- decimal.Decimal
The
decimal.Decimalrepresentation of the continued fraction.
Examples
Note that the default
decimalcontext precision of \(28\) is used in these examples.>>> import math >>> math.pi 3.141592653589793
Now construct a
ContinuedFractioninstance from it, and check thefloatvalue.>>> cf = ContinuedFraction(math.pi) >>> cf ContinuedFraction(884279719003555, 281474976710656) >>> cf.as_decimal() Decimal('3.141592653589793115997963469')
- property elements: tuple[int]#
The sequence of elements of the continued fraction.
Examples
>>> cf = ContinuedFraction('.12345') >>> cf ContinuedFraction(2469, 20000) >>> cf.elements (0, 8, 9, 1, 21, 1, 1, 5)
- Type:
- property order: int#
The order of the continued fraction, which is the number of its elements minus \(1\).
Examples
>>> cf = ContinuedFraction('.12345') >>> cf ContinuedFraction(2469, 20000) >>> len(cf.elements) 8 >>> cf.order 7
- Type:
- property khinchin_mean: Decimal | None#
The Khinchin mean of the continued fraction, which is defined as the geometric mean of all its elements after the 1st.
We define the Khinchin mean \(K_n\) of a simple continued fraction \([a_0; a_1, a_2, \ldots, a_n]\) as:
\[K_n := \sqrt[n]{a_1a_2 \cdots a_n} = \left( a_1a_2 \cdots a_n \right)^{\frac{1}{n}}, \hskip{3em} n \geq 1\]This property is intended to make it easier to study the limit of \(K_n\) as \(n \to \infty\). See the documentation for more details.
In the special case of integers or fractions representing integers, whose continued fraction representations consist of only a single element, a null value is returned.
Examples
Note that the default
decimalcontext precision of \(28\) is used in these examples.>>> ContinuedFraction(649, 200).elements (3, 4, 12, 4) >>> ContinuedFraction(649, 200).khinchin_mean Decimal('5.76899828122963409526846589869819581508636474609375') >>> ContinuedFraction(415, 93).elements (4, 2, 6, 7) >>> ContinuedFraction(415, 93).khinchin_mean Decimal('4.37951913988788898990378584130667150020599365234375') >>> (ContinuedFraction(649, 200) + ContinuedFraction(415, 93)).elements (7, 1, 2, 2, 2, 1, 1, 11, 1, 2, 12) >>> (ContinuedFraction(649, 200) + ContinuedFraction(415, 93)).khinchin_mean Decimal('2.15015313349074244086978069390170276165008544921875') >>> ContinuedFraction(5000).khinchin_mean
- Type:
- convergent(k: int, /) ContinuedFraction[source]#
Returns the \(k\)-th (simple) convergent of the continued fraction.
Given a simple continued fraction \([a_0;a_1,a_2,\ldots]\) the \(k\)-th convergent is defined as:
\[C_k = a_0 + \cfrac{1}{a_1 + \cfrac{1}{a_2 \ddots \cfrac{1}{a_{k-1} + \cfrac{1}{a_k}}}}\]The result is a
fractions.Fractioninstance.The integer \(k\) is called the order of the convergent, and if \([a_0;a_1,a_2,\ldots]\) is finite of order \(n\) then it has exactly \(n + 1\) convergents \(C_0,C_1,C_2,\ldots,C_n\) where the \(k\)-th convergent \(C_k = \frac{p_k}{q_k}\) is given by the recurrence relation:
\[\begin{split}\begin{align} p_k &= a_kp_{k - 1} + p_{k - 2} \\ q_k &= a_kq_{k - 1} + q_{k - 2}, \hskip{3em} k \geq 3 \end{align}\end{split}\]where \(p_0 = a_0\), \(q_0 = 1\), \(p_1 = p_1p_0 + 1\), and \(q_1 = p_1\).
The method is cached (with
functools.cache()), which makes calls after the initial call much faster.- Parameters:
- kint
The order of the convergent, as described above.
- Returns:
- ContinuedFraction
A new
ContinuedFractioninstance representing the \(k\)-th (simple) convergent of the original continued fraction, as described above.
Examples
>>> cf = ContinuedFraction('.12345') >>> cf ContinuedFraction(2469, 20000) >>> cf.convergent(0) ContinuedFraction(0, 1) >>> cf.convergent(2) ContinuedFraction(9, 73) >>> cf.convergent(6) ContinuedFraction(448, 3629) >>> cf.convergent(7) ContinuedFraction(2469, 20000)
- property convergents: mappingproxy[int, ContinuedFraction]#
An immutable dict of all \(k\)-order convergents of the continued fraction, keyed by order.
Each convergent is indexed by its order and is also a
ContinuedFractioninstance.The property is cached (with
functools.lru_cache()), which makes calls after the initial call much faster.Examples
>>> cf = ContinuedFraction('3.245') >>> cf.convergents mappingproxy({0: ContinuedFraction(3, 1), 1: ContinuedFraction(13, 4), 2: ContinuedFraction(159, 49), 3: ContinuedFraction(649, 200)}) >>> cf.convergents[0], cf.convergents[2] (ContinuedFraction(3, 1), ContinuedFraction(159, 49))
- Type:
- property even_order_convergents: mappingproxy[int, ContinuedFraction]#
An immutable dict of all even-order convergents of the continued fraction, keyed by order.
Each convergent is indexed by its order and is also a
ContinuedFractioninstance.The property is cached (with
functools.lru_cache()), which makes calls after the initial call much faster.Examples
>>> ContinuedFraction('3.245').even_order_convergents mappingproxy({0: ContinuedFraction(3, 1), 2: ContinuedFraction(159, 49)})
- Type:
- property odd_order_convergents: mappingproxy[int, ContinuedFraction]#
An immutable dict of all odd-order convergents of the continued fraction, keyed by order.
Each convergent is indexed by its order and is also a
ContinuedFractioninstance.The property is cached (with
functools.lru_cache()), which makes calls after the initial call much faster.Examples
>>> ContinuedFraction('3.245').odd_order_convergents mappingproxy({1: ContinuedFraction(13, 4), 3: ContinuedFraction(649, 200)})
- Type:
- remainder(k: int, /) ContinuedFraction[source]#
Returns the \(k\)-th remainder of the continued fraction.
The \(k\)-th remainder \(R_k\) of a (simple) continued fraction \([a_0; a_1,\ldots]\) as the continued fraction \([a_k;a_{k + 1},\ldots]\), obtained from the original by “removing” the elements of the \((k - 1)\)-st convergent \(C_{k - 1} = (a_0,a_1,\ldots,a_{k - 1})\).
\[R_k = a_k + \cfrac{1}{a_{k + 1} + \cfrac{1}{a_{k + 2} \ddots }}\]The method is cached (with
functools.cache()), which makes calls after the initial call much faster.- Parameters:
- kint
The index of the remainder, as described above.
- Returns:
- ContinuedFraction
A new
ContinuedFractioninstance representing the \(k\)-th remainder of the original continued fraction, as described above.
Examples
>>> cf = ContinuedFraction('.12345') >>> cf ContinuedFraction(2469, 20000) >>> cf.remainder(0) ContinuedFraction(2469, 20000) >>> cf.remainder(2) ContinuedFraction(2469, 248) >>> cf.remainder(6) ContinuedFraction(6, 5) >>> cf.remainder(7) ContinuedFraction(5, 1)
- property remainders: mappingproxy[int, ContinuedFraction]#
An immutable dict of all \(k\)-th remainders of the continued fraction, keyed by order.
Each remainder is indexed by its order and is also a
ContinuedFractioninstance.The property is cached (with
functools.lru_cache()), which makes calls after the initial call much faster.Examples
>>> cf = ContinuedFraction('3.245') >>> cf.remainders mappingproxy({0: ContinuedFraction(649, 200), 1: ContinuedFraction(200, 49), 2: ContinuedFraction(49, 4), 3: ContinuedFraction(4, 1)}) >>> cf.remainders[0], cf.remainders[2] (ContinuedFraction(649, 200), ContinuedFraction(49, 4))
- Type:
- left_mediant(other: Fraction, /, *, k: int = 1) ContinuedFraction[source]#
Returns the \(k\)-th left-mediant of the continued fraction with another rational number.
For a positive integer \(k\), the \(k\)-th left-mediant of two rational numbers \(r = \frac{a}{b}\) and \(s = \frac{c}{d}\), where \(b, d, b + d \neq 0\), is defined as:
\[\frac{ka + c}{kb + d}, \hskip{3em} k \geq 1\]while the \(k\)-th right mediant is defined as:
\[\frac{a + kc}{b + kd}, \hskip{3em} k \geq 1\]If we assume that \(r < s\) and \(bd > 0\) then these mediants have the property that:
\[\frac{a}{b} < \frac{ka + c}{kb + d} \leq \frac{a + kc}{b + kd} < \frac{c}{d}, \hskip{3em} k \geq 1\]where equality holds for \(k = 1\). If we let \(k \to \infty\) then the mediants converge to opposite limits:
\[\begin{split}\begin{align} \lim_{k \to \infty} \frac{ka + c}{kb + d} &= \frac{a}{b} \\ \lim_{k \to \infty} \frac{a + kc}{b + kd} &= \frac{c}{d} \end{align}\end{split}\]For more information consult the documentation.
The method is cached (with
functools.cache()), which makes calls after the initial call much faster.- Parameters:
- otherfractions.Fraction, ContinuedFraction
The second fraction to use to calculate the \(k\)-th mediant with the first.
- kint, default=1
The order of the mediant, as defined above.
- Returns:
- ContinuedFraction
The \(k\)-th left-mediant of the original fraction and the second fraction, as a
ContinuedFractioninstance.
Examples
>>> c1 = ContinuedFraction('1/2') >>> c2 = ContinuedFraction(3, 5) >>> c1, c2 (ContinuedFraction(1, 2), ContinuedFraction(3, 5)) >>> c1.left_mediant(c2) ContinuedFraction(4, 7) >>> c1.left_mediant(c2, k=2) ContinuedFraction(5, 9) >>> c1.left_mediant(c2, k=3) ContinuedFraction(6, 11) >>> c1.left_mediant(c2, k=100) ContinuedFraction(103, 205) >>> assert c1.left_mediant(c2, k=2) < c1.right_mediant(c2, k=2) >>> assert c1.left_mediant(c2, k=3) < c1.right_mediant(c2, k=3) >>> assert c1.left_mediant(c2, k=100) < c1.right_mediant(c2, k=100)
- right_mediant(other: Fraction, /, *, k: int = 1) ContinuedFraction[source]#
Returns the \(k\)-th right-mediant of the continued fraction with another rational number.
For a positive integer \(k\), the \(k\)-th right-mediant of two rational numbers \(r = \frac{a}{b}\) and \(s = \frac{c}{d}\), where \(b, d, b + d \neq 0\), is defined as:
\[\frac{a + kc}{b + kd}, \hskip{3em} k \geq 1\]while the \(k\)-th left-mediant is defined as:
\[\frac{ka + c}{kb + d}, \hskip{3em} k \geq 1\]If we assume that \(r < s\) and \(bd > 0\) then these mediants have the property that:
\[\frac{a}{b} < \frac{ka + c}{kb + d} \leq \frac{a + kc}{b + kd} < \frac{c}{d}, \hskip{3em} k \geq 1\]where equality holds for \(k = 1\). If we let \(k \to \infty\) then the mediants converge to opposite limits:
\[\begin{split}\begin{align} \lim_{k \to \infty} \frac{ka + c}{kb + d} &= \frac{a}{b} \\ \lim_{k \to \infty} \frac{a + kc}{b + kd} &= \frac{c}{d} \end{align}\end{split}\]For more information consult the documentation.
The method is cached (with
functools.cache()), which makes calls after the initial call much faster.- Parameters:
- otherfractions.Fraction, ContinuedFraction
The second fraction to use to calculate the \(k\)-th mediant with the first.
- kint, default=1
The order of the mediant, as defined above.
- Returns:
- ContinuedFraction
The \(k\)-th right-mediant of the original fraction and the second fraction, as a
ContinuedFractioninstance.
Examples
>>> c1 = ContinuedFraction('1/2') >>> c2 = ContinuedFraction(3, 5) >>> c1, c2 (ContinuedFraction(1, 2), ContinuedFraction(3, 5)) >>> c1.right_mediant(c2) ContinuedFraction(4, 7) >>> c1.right_mediant(c2, k=2) ContinuedFraction(7, 12) >>> c1.right_mediant(c2, k=3) ContinuedFraction(10, 17) >>> c1.right_mediant(c2, k=100) ContinuedFraction(301, 502) >>> assert c1.left_mediant(c2, k=2) < c1.right_mediant(c2, k=2) >>> assert c1.left_mediant(c2, k=3) < c1.right_mediant(c2, k=3) >>> assert c1.left_mediant(c2, k=100) < c1.right_mediant(c2, k=100)