`continuedfractions.lib`#

continuedfractions.lib.continued_fraction_real(x: int | float | str | Decimal, /) → Generator[int, None, None][source]#

Generates elements/coefficients of a simple continued fraction of the given real number.

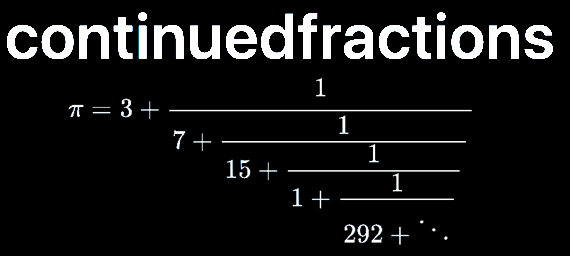
The simple continued fraction representation of \(x\) is a number of the form

\[a_0 + \cfrac{1}{a_1 + \cfrac{1}{a_2 + \ddots}}\]

where \(a_0 = [x]\) is the integer part of \(x\), and the \(a_1,a_2\ldots\) are the (non-negative) quotients obtained by a repeated application of Euclidean division to the fractional part \(x - [x]\), which is called the remainder.

As Python float values, like all floating point implementations, are finite precision representations of real numbers, the resulting simple continued fraction of \(x\) generated by this function may be approximate, not exact, and also not necessarily unique.

For non-rational real numbers it is best to pass decimal.Decimal values, with the context precision set to the highest level possible.

The results for rational numbers are guaranteed to be exact however large the number, subject to memory and hardware limitations of the running environment.

Invalid values will generate an error in either the fractions.Fraction or decimal.Decimal classes - no errors are raised directly in the function itself.

Parameters:

xint, float, str, decimal.Decimal: The real number to represent as a simple continued fraction.

Yields:

int: Elements of a simple continued fraction of the given real number.

Examples

A few examples are given below of how this function can be used.

>>> list(continued_fraction_real(5000))
[5000]
>>> list(continued_fraction_real(-5000.0))
[-5000]
>>> list(continued_fraction_real(2/5))
[0, 2, 2, 1801439850948198]
>>> list(continued_fraction_real('2/5'))
[0, 2, 2]
>>> list(continued_fraction_real('-1/3'))
[-1, 1, 2]
>>> list(continued_fraction_real(1/1j))
Traceback (most recent call last):
...
TypeError: conversion from complex to Decimal is not supported
>>> list(continued_fraction_real("not a numeric string"))
Traceback (most recent call last):
...
decimal.InvalidOperation: [<class 'decimal.ConversionSyntax'>]
>>> list(continued_fraction_real(-649/200))
[-4, 1, 3, 12, 3, 1, 234562480591, 2, 5, 2]
>>> list(continued_fraction_real('-649/200'))
[-4, 1, 3, 12, 4]
>>> list(continued_fraction_real('-649/-200'))
Traceback (most recent call last):
...
ValueError: Invalid literal for Fraction: '-649/-200'
>>> list(continued_fraction_real(Decimal('0.3333')))
[0, 3, 3333]

continuedfractions.lib.continued_fraction_rational(r: Fraction, /) → Generator[int, None, None][source]#

Generates elements/coefficients of the finite, simple continued fraction for the given rational number.

The resulting sequence of elements defines a continued fraction of the form:

\[a_0 + \cfrac{1}{a_1 + \cfrac{1}{a_2 + \ddots\cfrac{1}{a_{n - 1} + \cfrac{1}{a_n}}}}\]

which is also written more compactly as:

\[[a_0; a_1, a_2\ldots, a_n]\]

The order of the continued fraction is said to be \(n\).

Negative rational numbers can also be represented in this way, provided we use the Euclidean division lemma. This is described in more detail in the documentation.

For a definition of “continued fraction”, “element”, “order”, “finite continued fraction”, “simple continued fraction”, please consult the package documentation, or any online resource such as Wikipedia, or suitable books on number theory.

Parameters:

rfractions.Fraction: The rational number to represented as a continued fraction.

Yields:

int: Elements of a unique, finite “simple” continued fraction representation of the given rational number.

Notes

Every rational number has exactly two simple continued fractions, one of which has an additional element of \(1\) as its last element, i.e. \([a_0;a_1,a_2,\ldots,a_{n - 1}, 1]\). But this form can be reduced by adding the \(1\) to the second last element, \(a_{n - 1}\), producing the shorter form \([a_0;a_1,a_2,\ldots, a_{n - 1} + 1]\), where the last element is now \(> 1\).

The simple continued fraction representation generated by this function is the shorter version, and is thus unique.

Examples

A few examples are given below of how this function can be used.

>>> for e in continued_fraction_rational(Fraction(649, 200)):
...     print(e)
...
3
4
12
4
>>> list(continued_fraction_rational(Fraction(415, 93)))
[4, 2, 6, 7]
>>> list(continued_fraction_rational(Fraction(-649, 200)))
[-4, 1, 3, 12, 4]
>>> list(continued_fraction_rational(Fraction(123235, 334505)))
[0, 2, 1, 2, 1, 1, 250, 1, 13]

continuedfractions.lib.convergent(k: int, *elements: int) → Fraction[source]#

Returns the \(k\)-th convergent of a simple continued fraction from a sequence of its elements.

Given a simple continued fraction \([a_0;a_1,a_2,\ldots]\) the \(k\)-th convergent is defined as:

\[C_k = a_0 + \cfrac{1}{a_1 + \cfrac{1}{a_2 \ddots \cfrac{1}{a_{k-1} + \cfrac{1}{a_k}}}}\]

The result is a fractions.Fraction instance.

The integer \(k\) is called the order of the convergent, and if \([a_0;a_1,a_2,\ldots]\) is finite of order \(n\) then it has exactly \(n + 1\) convergents \(C_0,C_1,C_2,\ldots,C_n\) where the \(k\)-th convergent \(C_k = \frac{p_k}{q_k}\) is given by the recurrence relation:

\[\begin{split}\begin{align} p_k &= a_kp_{k - 1} + p_{k - 2} \\ q_k &= a_kq_{k - 1} + q_{k - 2}, \hskip{3em} k \geq 3 \end{align}\end{split}\]

where \(p_0 = a_0\), \(q_0 = 1\), \(p_1 = p_1p_0 + 1\), and \(q_1 = p_1\).

This function is a faithful implementation of this algorithm.

A ValueError is raised if \(k\) is not an integer or is an integer greater than the number of elements, or if any of the elements are not integers.

Parameters:

kint: The order of the convergent. Must be a non-negative integer less than the number of elements.
*elementsint: A variable-length sequence of integer elements of a continued fraction.

Returns:

fractions.Fraction: A rational fraction constructed from the given sequence of elements of a continued fraction, representing the \(k\)-order convergent of a (finite) simple continued fraction as given by a sequence of elements.

Raises:

ValueError: If \(k\) is not a non-negative integer less than the number of elements, or if any of the elements are not integers.

Examples

>>> convergent(0, 3, 4, 12, 4)
Fraction(3, 1)
>>> convergent(1, 3, 4, 12, 4)
Fraction(13, 4)
>>> convergent(2, 3, 4, 12, 4)
Fraction(159, 49)
>>> convergent(3, 3, 4, 12, 4)
Fraction(649, 200)
>>> convergent(-1, 3, 4, 12, 4)
Traceback (most recent call last):
...
ValueError: `k` must be a non-negative integer less than the number of
elements of the continued fraction.
>>> convergent(4, 3, 4, 12, 4)
Traceback (most recent call last):
...
ValueError: `k` must be a non-negative integer less than the number of
elements of the continued fraction.

continuedfractions.lib.fraction_from_elements(*elements: int) → Fraction[source]#

Returns the rational number represented by a simple (finite) continued fraction from a sequence of its elements.

The elements must be given as positional arguments, which means that if they are contained in an iterable then they must be unpacked using the unpacking operator *, as described in the examples below.

Parameters:

*elementsint: A variable-length sequence of integer elements of a simple continued fraction.

Returns:

fractions.Fraction: A rational number constructed from a sequence of elements of a simple continued fraction which represents the number.

Raises:

ValueError: If any of the elements are not integers.

Examples

>>> fraction_from_elements(3, 4, 12, 4)
Fraction(649, 200)
>>> fraction_from_elements(-4, 1, 3, 12, 4)
Fraction(-649, 200)
>>> fraction_from_elements(4, 2, 6, 7)
Fraction(415, 93)
>>> fraction_from_elements(*[4, 2, 6, 7])
Fraction(415, 93)
>>> fraction_from_elements(4.5, 2, 6, 7)
Traceback (most recent call last):
...
ValueError: Continued fraction elements must be integers

continuedfractions.lib.left_mediant(r: Fraction, s: Fraction, /, *, dir: str = 'left', k: int = 1) → Fraction#: A functools.partial() binding of mediant() for left-mediants.

continuedfractions.lib.mediant(r: Fraction, s: Fraction, /, *, dir: str = 'right', k: int = 1) → Fraction[source]#

Returns the \(k\)-th left- or right-mediant of two rational numbers.

For a positive integer \(k\), the \(k\)-th left-mediant of two rational numbers \(r = \frac{a}{b}\) and \(s = \frac{c}{d}\), where \(b, d, b + d \neq 0\), is defined as:

\[\frac{ka + c}{kb + d}, \hskip{3em} k \geq 1\]

while the \(k\)-th right mediant is defined as:

\[\frac{a + kc}{b + kd}, \hskip{3em} k \geq 1\]

If we assume that \(r < s\) and \(bd > 0\) then these mediants have the property that:

\[\frac{a}{b} < \frac{ka + c}{kb + d} \leq \frac{a + kc}{b + kd} < \frac{c}{d}, \hskip{3em} k \geq 1\]

where equality holds for \(k = 1\). If we let \(k \to \infty\) then the mediants converge to opposite limits:

\[\begin{split}\begin{align} \lim_{k \to \infty} \frac{ka + c}{kb + d} &= \frac{a}{b} \\ \lim_{k \to \infty} \frac{a + kc}{b + kd} &= \frac{c}{d} \end{align}\end{split}\]

For more information consult the documentation.

For the left mediant use dir="left", while for the right use dir="right". The default is dir="right". For k = 1 the left and right mediants are identical to the simple mediant \(\frac{a + c}{b + d}\).

Parameters:

rfractions.Fraction: The first rational number.
sfractions.Fraction: The second rational number.
dirstr, default=’right’: The “direction” of the mediant - ‘left’ or ‘right’, as defined above.
kint, default=1: The order of the mediant, as defined above.

Returns:

fractions.Fraction: The k-th left- or right-mediant of the two given rational numbers.

Examples

>>> mediant(Fraction(1, 2), Fraction(3, 5))
Fraction(4, 7)
>>> mediant(Fraction(1, 2), Fraction(3, 5), dir='left')
Fraction(4, 7)
>>> mediant(Fraction(1, 2), Fraction(3, 5), k=2)
Fraction(7, 12)
>>> mediant(Fraction(1, 2), Fraction(3, 5), dir='left', k=2)
Fraction(5, 9)
>>> mediant(Fraction(1, 2), Fraction(3, 5), k=3, dir='right')
Fraction(10, 17)
>>> mediant(Fraction(1, 2), Fraction(3, 5), k=3, dir='left')
Fraction(6, 11)

continuedfractions.lib.right_mediant(r: Fraction, s: Fraction, /, *, dir: str = 'right', k: int = 1) → Fraction#: A functools.partial() binding of mediant() for right-mediants.

continuedfractions.lib#

`continuedfractions.lib`#