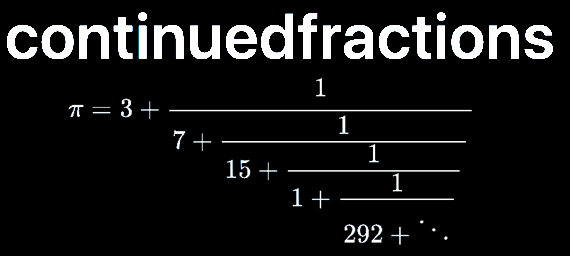
Creating Continued Fractions#
It’s useful to start with the basic mathematics of continued fractions, using a simple example.
The Basic Math#
Consider the rational number \(\frac{649}{200} = \frac{3 \times 200 + 49}{200} = 3.245\) which has a continued fraction representation, or simply, a continued fraction, given by:
This is derived by repeatedly applying Euclid’s division lemma, as described below:
The numbers \(3, 4, 12, 4\) are called elements (or coefficients) of the continued fraction \([3; 4, 12, 4]\), and the number of elements after the first - in this case \(3\) - is defined to be its order.
The representation \([3; 4, 12, 4]\) is called simple (or regular) because all of the numerators in the fractional terms are equal to \(1\), which makes the fractions irreducible (cannot be simplified further). Mathematically, the continued fraction is written as \([3; 4, 12, 4]\). The representation is also unique - the only other representation is \([3; 4, 12, 3, 1]\), which can be rewritten as \([3; 4, 12, 4]\).
Note
All references to continued fractions are to the simple forms where the last element \(> 1\).
Support for non-simple, generalised continued fractions is planned to be included in future releases.
We can think of \(3\), which is the integer part of \(\frac{649}{200} = 3.245\), as the “head” of the continued fraction, and the integers \(4, 12, 4\), which determine the fractional part \(\cfrac{1}{4 + \cfrac{1}{12 + \cfrac{1}{4}}} = \frac{49}{200} = 0.245\) of the continued fraction, as its “tail”.
Creating Continued Fractions from Numeric Types#
Import the core class continuedfractions.continuedfraction.ContinuedFraction.
>>> from continuedfractions.continuedfraction import ContinuedFraction
The ContinuedFraction instance for \(\frac{649}{200}\) can be created as follows.
>>> cf = ContinuedFraction(649, 200)
>>> cf
ContinuedFraction(649, 200)
Note
The same instance can also be constructed using ContinuedFraction('649/200'), ContinuedFraction('3.245'), ContinuedFraction(Fraction(649, 200)), ContinuedFraction(Fraction(649), 200)), ContinuedFraction(649, Fraction(200))), and ContinuedFraction(Decimal('3.245')), and even ContinuedFraction(ContinuedFraction(649, 200)) .
But passing a numeric literal such as 649/200 will result in an evaluation of the decimal integer division using binary floating point division, thus producing a fractional approximation, in this case, ContinuedFraction(3653545197704315, 1125899906842624).
The float value of ContinuedFraction(649, 200) is available via the as_float() method, in this case, a value of \(3.245\).
>>> cf.as_float()
3.245
A decimal.Decimal value of ContinuedFraction(649, 200) is also available via the as_decimal() method.
>>> cf.as_decimal()
Decimal('3.245')
Decimal Precision#
The Python decimal library can, in principle, support arbitrary precision arithmetic, subject to the limitations of the running environment, system, hardware etc. It does this via context objects for Decimal instances, in which you can set the precision of the Decimal values in your current environment to whatever is appropriate to your computation or experiment, subject to the limitations of your environment and/or system.
An example is given below:
# Inspect the current context
>>> decimal.getcontext()
Context(prec=28, rounding=ROUND_HALF_EVEN, Emin=-999999, Emax=999999, capitals=1, clamp=0, flags=[Inexact, Rounded], traps=[InvalidOperation, DivisionByZero, Overflow])
>>> Decimal('1') / 3
Decimal('0.3333333333333333333333333333')
# Increase the precision to 100 digits, including the integer part of the number
>>> decimal.getcontext().prec = 100
>>> Decimal('1') / 3
Decimal('0.3333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333')
Note
This doesn’t necessarily work for all float values, e.g. math.pi, or math.sqrt(2), so be careful.
You can also set indicators that Decimal computations should be exact, and trigger signals if results are not exact and that some kind of rounding was applied - see the Decimal FAQ for more information and examples.
Irrational Numbers#
Every finite continued fraction represents a rational number, as a finite continued fraction is a “nested” sum of rational numbers. Conversely, every rational number can be represented as a finite (and simple) continued fraction, by an iterative procedure using Euclidean division. On the other hand, infinite continued fractions represent irrational numbers and conversely every infinite continued fraction represents an irrational number.
There are infinitely many rational and irrational numbers that cannot be represented exactly as binary fractions, which form the basis for floating point arithmetic, and, therefore, also, cannot be represented exactly as Python float instances. To deal with this, the package processes rational numbers using the fractions.Fraction class, which allows for exact continued fractions for any rational number, limited only by the available memory and/or capacity of the running environment.
Continued fractions for irrational numbers given directly as float instances end up as fractional approximations, as they rely on converting decimal.Decimal representations of the given float value to a fractions.Fraction instance. However, as described in the next section, the from_elements() method can be used to create ContinuedFraction instances with arbitrary sequences of elements, which can give much more accurate results.
An example is given below for the irrational \(\sqrt{2}\), which is given by the infinite periodic continued fraction \([1; 2, 2, 2, \ldots]\). We first begin by constructing the ContinuedFraction instance for \(\sqrt{2}\) directly from a math.sqrt(2) value:
>>> sqrt2 = ContinuedFraction(math.sqrt(2))
>>> sqrt2
ContinuedFraction(6369051672525773, 4503599627370496)
>>> sqrt2.elements
# -> (1, 2, 2, 2, 2, ... ,1, 1, 10, 2, ... ,1, 3, 1, 17, 12, 3, 2, 6, 1, 11, 2, 2)
>>> sqrt2.as_float()
1.4142135623730951
>>> sqrt2.as_decimal()
Decimal('1.4142135623730951454746218587388284504413604736328125')
>>> Decimal(math.sqrt(2)).as_integer_ratio()
Fraction(6369051672525773, 4503599627370496)
Here, ContinuedFraction(6369051672525773, 4503599627370496) is a fractional approximation of \(\sqrt{2}\), for the reasons described above, and not exact, as reflected in the tail elements of the sequence deviating from the mathematically correct value of \(2\). Also, note that the decimal value of ContinuedFraction(math.sqrt(2)) above for \(\sqrt{2}\) is only accurate up to \(15\) digits in the fractional part, compared to the first one million digit representation.
However, in the next section, we describe a way to construct continued fractions with arbitary sequences of elements, which can produce results of any given desired level of accuracy for irrational numbers.
Creating Continued Fractions From Elements/Coefficients#
Continued fractions can also be constructed from sequences of elements, using the from_elements() class method.
>>> cf = ContinuedFraction.from_elements(3, 4, 12, 4)
>>> cf
ContinuedFraction(649, 200)
>>> cf_inverse = ContinuedFraction.from_elements(0, 3, 4, 12, 4)
>>> cf_inverse
ContinuedFraction(200, 649)
>>> cf_negative_inverse = ContinuedFraction.from_elements(-1, 1, 2, 4, 12, 4)
>>> cf_negative_inverse
ContinuedFraction(-200, 649)
>>> cf_negative_inverse.elements
(-1, 1, 2, 4, 12, 4)
The given sequence of elements can be arbitrarily long, subject to the limitations of the environment, system etc. Here is an example for approximating \(\sqrt{2}\) with \([1; \overbrace{2, 2,\ldots, 2]}^{1000 \text{ twos}}\) where the tail contains \(1000\) twos.
>>> decimal.getcontext().prec = 1000
>>> ContinuedFraction.from_elements(1, *[2] * 1000).as_decimal()
>>> Decimal('1.414213562373095048801688724209698078569671875376948073176679737990732478462107038850387534327641572735013846230912297024924836055850737212644121497099935831413222665927505592755799950501152782060571470109559971605970274534596862014728517418640889198609552329230484308714321450839762603627995251407989687253396546331808829640620615258352395054745750287759961729835575220337531857011354374603408498847160386899970699004815030544027790316454247823068492936918621580578463111596668713013015618568987237235288509264861249497715421833420428568606014682472077143585487415565706967765372022648544701585880162075847492265722600208558446652145839889394437092659180031138824646815708263010059485870400318648034219489727829064104507263688131373985525611732204024509122770022693976417470272013752399982976782217338826145327739130951193355408762382855063050397471264684204993755563270525522588635793369056816493299408349652485293806821732869748392205646382061385126800425762739265218823406558704964782626829881122')
The algorithm implemented by from_elements() is division-free and uses a well known recurrence relation for convergents of simple continued fractions, which is described here.
For rational numbers from_elements() will produce exactly the same results as the constructor for ContinuedFraction, but with the benefit of allowing the user to specify an exact sequence of elements, if it is known, or an arbitrary sequence of elements for approximations or experimental computations.
Rational Operations#
The ContinuedFraction class is a subclass of fractions.Fraction and supports all of the rational operations implemented in the superclass. This means that ContinuedFraction instances are fully operable as rational numbers, as well as encapsulating the properties of (finite) simple continued fractions.
Note
Implementations of rational operations in the ContinuedFraction class will always return a ContinuedFraction instance unless the operation is binary and the other operand is either not a fractions.Fraction instance, or in some operations, such as __pow__(), __rpow__() etc., not an int.
A few examples are given below of some key rational operations for the rational \(\frac{649}{200}\) with ContinuedFraction(649, 200).
>>> cf = ContinuedFraction.from_elements(3, 4, 12, 4)
>>> cf
ContinuedFraction(649, 200)
>>> cf.elements
(3, 4, 12, 4)
>>> cf_inverse = ContinuedFraction.from_elements(0, 3, 4, 12, 4)
>>> cf_inverse
ContinuedFraction(200, 649)
>>> cf_inverse.elements
(0, 3, 4, 12, 4)
>>> assert cf_inverse == 1/cf
# True
>>> assert cf * cf_inverse == 1
# True
>>> cf_negative_inverse = ContinuedFraction.from_elements(-1, 1, 2, 4, 12, 4)
>>> cf_negative_inverse
ContinuedFraction(-200, 649)
>>> cf_negative_inverse.elements
(-1, 1, 2, 4, 12, 4)
>>> assert cf_negative_inverse == -1/cf
# True
>>> assert cf * cf_negative_inverse == -1
>>> assert cf + (-cf) == cf_inverse + cf_negative_inverse == 0
# True
>>> cf ** 2
ContinuedFraction(421201, 40000)
>>> (cf ** 2).elements
(10, 1, 1, 7, 1, 4, 1, 3, 5, 1, 7, 2)
>>> assert ContinuedFraction.from_elements(10, 1, 1, 7, 1, 4, 1, 3, 5, 1, 7, 2) == cf ** 2
# True
As these examples illustrate, the continued fraction properties of the ContinuedFraction instances are fully respected by the rational operations.
Rational operations for ContinuedFraction can involve any instance of numbers.Rational, including int and fractions.Fraction, but results are only guaranteed for the latter two types, and in these cases the result is always a new ContinuedFraction instance.
>>> cf = ContinuedFraction('0.5')
>>> cf
ContinuedFraction(1, 2)
>>> id(cf), id(-cf)
(4603182592, 4599771072)
There is no support for binary operations involving decimal.Decimal:
>>> ContinuedFraction('1.5') + Decimal('0.5')
TypeError: unsupported operand type(s) for +: 'decimal.Decimal' and 'Fraction'
For any other numeric type, such as complex, if the operation is defined the result is not a ContinuedFraction instance:
>>> complex(1, 2) + ContinuedFraction(3, 2)
(2.5+2j)
The full set of rational operations can be viewed directly in the class source - the class source also can be viewed from links in the class API reference.
“Negative” Continued Fractions#
Continued fractions for negative numbers can be derived, provided we use Euclidean integer division to calculate the elements of the representation, by starting with the integer part of the number, and then calculating the remaining elements for the fractional part with the successive quotients and remainders obtained in each division step. For example, \(\frac{-415}{93} = \frac{-5 \times 93 + 50}{93}\) has the (unique) simple continued fraction \([-5; 1, 1, 6, 7]\):
Compare this with \([4; 2, 6, 7]\), which is the simple continued fraction of \(\frac{415}{93} = \frac{4 \times 93 + 43}{93}\):
To understand the difference in the sequence of elements between a “positive” and “negative” continued fraction, more generally, we can start by applying Euclid’s division lemma to a positive rational number \(\frac{a}{b}\), with \(b < a\) and \(a, b\) coprime (no common divisors except \(1\)). Let \([a_0;a_1,\ldots,a_n]\) be the simple continued fraction of order \(n \geq 1\) of \(\frac{a}{b}\), where we can assume \(a_n > 1\). The lemma implies that there are unique, positive integers \(q, v\), with \(0 < v < b\), such that \(a = qb + v\). Then:
where \(R_1 = [a_1; a_2, \ldots, a_n]\) is the “residual”, \((n - 1)\)-order simple continued fraction of \(\frac{b}{v}\), also called the 1st remainder of the continued fraction \([a_0;a_1,\ldots,a_n]\) of \(\frac{a}{b}\). If \(v = 1\) then \(R_1 = [b;]\) and \([q; b]\) is the simple continued fraction of \(\frac{a}{b}\). However, if \(v > 1\) then \(R_1\) is defined and \(\frac{1}{R_1}\) is a symbolic expression for the rational number which is the (multiplicative) inverse of the rational number represented by \(R_1\).
Note
For integers \(0 < b < a\), if \(\frac{a}{b}\) (\(> 1\)) has the simple continued fraction \([a_0; a_1, \ldots, a_n]\) of order \(n\), then \(0 < \frac{b}{a} < 1\) has the “inverted” simple continued fraction \([0; a_0, a_1, \ldots, a_n]\) of order \(n + 1\). Both are unique if \(a_n > 1\).
Also, if \(m\) is any integer then \(m + [a_0;a_1,\ldots, a_n] = [a_0;a_1,\ldots, a_n] + m\) is a symbolic expression for \([m;] + [a_0;a_1,\ldots, a_n] = [a_0;a_1,\ldots, a_n] + [m;] = [a_0 + m;a_1,\ldots, a_n]\), where \([m;]\) is the continued fraction of \(m\).
We can write \(-a = -(qb + v)\) as:
so that:
where \(R_1 - 1 = [a_1 - 1;a_2,\ldots, a_n]\) and \(\frac{1}{R_1 - 1} = [0; a_1 - 1, a_2, a_3,\ldots, a_n]\).
Note
If the last element \(a_n = 1\) then \([a_0; a_1, \ldots, a_n] = [a_0;a_1,\ldots,a_{n - 1} + 1]\) is of order \((n - 1)\). So in the representation \([-(q + 1); 1, a_1 - 1, a_2, a_3,\ldots, a_n]\) above for \(-\frac{a}{b}\), if \(a_1 = 2\) then \(a_1 - 1 = 1\) and the segment \([-(q + 1); 1, a_1 - 1] = [-(q + 1); 1, 1] = [-(q + 1); 2]\) is of order \(1\).
If \(\bar{R}_1\) denotes the 1st remainder \([1; a_1 - 1, a_2, a_3,\ldots, a_n]\) in the representation above for \(-\frac{a}{b}\) then \(\bar{R}_1\) is an \(n\)-order, simple continued fraction. A special case is when \(a_1 = 1\): in this case \(a_0 = -1\) and \(\bar{R}_1 = [a_2 + 1; a_3, \ldots, a_n]\) is an \((n - 2)\)-order simple continued fraction. Note that this special case also applies when \(0 < a < b\).
Thus, we can say that if \([a_0; a_1,\ldots, a_n]\) is the \(n\)-order simple continued fraction of a positive rational number \(\frac{a}{b}\) then the simple continued fraction of \(-\frac{a}{b}\) is given by:
This represents a division-free algorithm for computing the simple continued fraction of the negative of a positive rational number, and is faithfully implemented in the __neg__() method.
Note
This algorithm can be combined with the basic rule for the simple continued fraction of the multiplicative inverse of a given positive rational number to yield division-free algorithms for computing simple continued fractions for multiplying and dividing pairs of rational numbers, and also for taking exponents of rational numbers with integers. These will be implemented in ContinuedFraction in future releases.
We can illustrate the negation relations above with ContinuedFraction instances for small fractions \(\frac{a}{b}\) where \(|a| < |b|\):
>>> ContinuedFraction(2, 3).elements
(0, 1, 2)
>>> ContinuedFraction(-2, 3).elements
(-1, 3)
>>> assert ContinuedFraction.from_elements(-1, 3) == ContinuedFraction(-2, 3)
# True
>>> ContinuedFraction(1, 2).elements
(0, 2)
>>> ContinuedFraction(-1, 2).elements
(-1, 2)
>>> assert ContinuedFraction.from_elements(-1, 2) == ContinuedFraction.from_elements(-1, 1, 1) == ContinuedFraction(-1, 2)
# True
and also fractions \(\frac{a}{b}\) where \(|a| > |b|\):
>>> ContinuedFraction(17, 10).elements
(1, 1, 2, 3)
>>> ContinuedFraction(-17, 10).elements
(-2, 3, 3)
>>> assert ContinuedFraction.from_elements(-2, 3, 3) == ContinuedFraction(-17, 10)
# True
>>> ContinuedFraction(10, 7).elements
(1, 2, 3)
>>> ContinuedFraction(-10, 7).elements
(-2, 1, 1, 3)
>>> assert ContinuedFraction.from_elements(-2, 1, 1, 3) == ContinuedFraction(-10, 7)
# True
The construction (creation + initialisation) of ContinuedFraction instances occurs mostly in the fractions.Fraction class, but there are no sign-related differences either in the construction steps in __new__().
A few examples are given below.
>>> ContinuedFraction(-415, 93)
ContinuedFraction(-415, 93)
>>> -ContinuedFraction(415, 93)
ContinuedFraction(-415, 93)
>>> ContinuedFraction(-415, 93).elements
(-5, 1, 1, 6, 7)
>>> ContinuedFraction(-415, 93).convergents
mappingproxy({0: Fraction(-5, 1), 1: Fraction(-4, 1), 2: Fraction(-9, 2), 3: Fraction(-58, 13), 4: Fraction(-415, 93)})
>>> ContinuedFraction(-415, 93).as_decimal()
Decimal('-4.462365591397849462365591397849462365591397849462365591397849462365591397849462365591397849462365591')
>>> ContinuedFraction(415, 93).as_decimal()
Decimal('4.462365591397849462365591397849462365591397849462365591397849462365591397849462365591397849462365591')
Note
As negation of numbers is a unary operation, the minus sign in a “negative” ContinuedFraction instance must be attached to the fraction, before enclosure in parentheses.
>>> -ContinuedFraction(415, 93).elements
...
TypeError: bad operand type for unary -: 'tuple'
>>> -(ContinuedFraction(415, 93)).elements
...
TypeError: bad operand type for unary -: 'tuple'
>>> (-ContinuedFraction(415, 93)).elements
(-5, 1, 1, 6, 7)
>>> assert ContinuedFraction(415, 93) + (-ContinuedFraction(415, 93)) == 0
# True
References#
[1] Baker, Alan. A concise introduction to the theory of numbers. Cambridge: Cambridge Univ. Pr., 2002.
[2] Barrow, John D. “Chaos in Numberland: The secret life of continued fractions.” plus.maths.org, 1 June 2000, https://plus.maths.org/content/chaos-numberland-secret-life-continued-fractionsURL.
[3] Emory University Math Center. “Continued Fractions.” The Department of Mathematics and Computer Science, https://mathcenter.oxford.emory.edu/site/math125/continuedFractions/. Accessed 19 Feb 2024.
[4] Khinchin, A. Ya. Continued Fractions. Dover Publications, 1997.
[5] NASA. “The Square Root of Two to 1 Million Digits”. Astronomy Picture of the Day, https://apod.nasa.gov/htmltest/gifcity/sqrt2.1mil. Accessed 13 March 2024.
[6] Python 3.12.2 Docs. “decimal - Decimal fixed point and floating point arithmetic.” https://docs.python.org/3/library/decimal.html. Accessed 21 February 2024.
[7] Python 3.12.2 Docs. “Floating Point Arithmetic: Issues and Limitations.” https://docs.python.org/3/tutorial/floatingpoint.html. Accessed 20 February 2024.
[8] Python 3.12.2 Docs. “fractions - Rational numbers.” https://docs.python.org/3/library/fractions.html. Accessed 21 February 2024.
[9] Wikipedia. “Continued Fraction”. https://en.wikipedia.org/wiki/Continued_fraction. Accessed 19 February 2024.