Ctrl+K

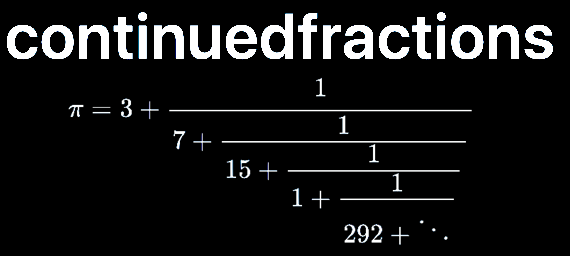
Mediants#

Another feature which the package includes is mediants, which are useful not for only approximations but also have very interesting connections to other areas of number theory, including ordered sequences of rational numbers.

Mediants and their Properties#

The (simple) mediant of two rational numbers \(\frac{a}{b}\) and \(\frac{c}{d}\), where \(b, d, b + d \neq 0\), is defined as the rational number:

\[\frac{a + c}{b + d}\]

Assuming that \(\frac{a}{b} < \frac{c}{d}\) and \(bd > 0\) (which implies both \(\frac{a}{b}\) and \(\frac{c}{d}\) have the same sign) the mediant above has the property that:

\[\frac{a}{b} < \frac{a + c}{b + d} < \frac{c}{d}\]

From the assumptions above this can be proved easily from the following relations:

\[\begin{split}\begin{align} \frac{a}{b} < \frac{c}{d} &\iff \frac{c}{a} > \frac{d}{b} \iff \frac{a}{c} < \frac{b}{d} \\ \frac{a + c}{b + d} &= \frac{a}{b} \cdot \frac{1 + \frac{c}{a}}{1 + \frac{d}{b}} \\ &= \frac{c}{d} \cdot \frac{1 + \frac{a}{c}}{1 + \frac{b}{d}} \end{align}\end{split}\]

Mediants can give good rational approximations to real numbers.

The ContinuedFraction class provides a right_mediant() method which can be used to calculate (simple) mediants with other ContinuedFraction or fractions.Fraction instances. The result is also a ContinuedFraction instance. A few examples are given below of how to calculate mediants.

>>> ContinuedFraction('0.5').right_mediant(Fraction(2, 3))
ContinuedFraction(3, 5)
>>> ContinuedFraction('0.6').elements
(0, 1, 1, 2)
>>> ContinuedFraction(1, 2).right_mediant(ContinuedFraction('2/3'))
ContinuedFraction(3, 5)
>>> assert ContinuedFraction(1, 2) < ContinuedFraction(1, 2).right_mediant(Fraction(3, 4)) < ContinuedFraction(3, 4)
# True

There is also a corresponding left_mediant() method, which gives you the same value for \(k = 1\). The definitions of “right-mediant” and “left-mediant” are given in the next section, but the right_mediant() is sufficient for computing simple mediants.

In particular, the mediant \(\frac{a + c}{b + d}\) of \(\frac{a}{b}\) and \(\frac{c}{d}\) has the property that if \(bc - ad = 1\) then \(\frac{a + c}{b + d}\) is the fraction with the smallest denominator lying in the (open) interval \((\frac{a}{b}, \frac{c}{d})\). As \(\frac{1}{2}\) and \(\frac{2}{3}\) satisfy the relation \(bc - ad = 2\cdot2 - 1\cdot3 = 4 - 3 = 1\) it follows that their mediant \(\frac{3}{5}\) is the “next” (or “first”) fraction after \(\frac{1}{2}\), but before \(\frac{2}{3}\), compared to any other fraction in that interval with a denominator \(\geq b + d = 5\).

This is an ordering property that links mediants to ordered sequences of rational numbers such as Farey sequences, and tree orderings such as the Stern-Brocot tree.

Generalised Mediants#

The concept of the simple mediant of two fractions of \(\frac{a}{b}\) and \(\frac{c}{d}\) as given above can be generalised to \(k\)-th left- and right-mediants: for a positive integer \(k\) the \(k\)-th left mediant of \(\frac{a}{b}\) and \(\frac{c}{d}\) can be defined as:

\[\frac{ka + c}{kb + d}, \hskip{3em} k \geq 1\]

while the \(k\)-th right mediant can be defined as:

\[\frac{a + kc}{b + kd}, \hskip{3em} k \geq 1\]

For \(k = 1\) the left- and right-mediants are identical to the simple mediant \(\frac{a + c}{b + d}\), but for \(k > 1\) the \(k\)-th left-mediant is less than the \(k\)-th right mediant. Using the assumptions \(\frac{a}{b} < \frac{c}{d}\) and \(bd > 0\), the proof is given by:

\[\begin{split}\begin{align} \frac{a + kc}{b + kd} - \left(\frac{ka + c}{kb + d}\right) &= \frac{(a + kc)(kb + d) - (b + kd)(ka + c)}{(b + kd)(kb + d)} \\ &= \frac{k^2(bc - ad) - (bc - ad)}{(b + kd)(kb + d)} \\ &= \frac{(bc - ad)(k^2 - 1)}{(b + kd)(kb + d)} \\ &\geq 0 \end{align}\end{split}\]

where equality holds if and only if \(k = 1\).

Left- and right-mediants can be constructed easily using the ContinuedFraction class, which provides the left_mediant() and right_mediant() methods.

Here are some examples of constructing left-mediants:

>>> cf1 = ContinuedFraction('1/2')
>>> cf2 = ContinuedFraction(3, 5)
# The default `k = 1` gives you the common, simple mediant of the two rationals
>>> cf1.left_mediant(c2)
ContinuedFraction(4, 7)
>>> cf1.left_mediant(cf2, k=2)
ContinuedFraction(5, 9)
>>> cf1.left_mediant(cf2, k=100)
ContinuedFraction(103, 205)
>>> cf1.left_mediant(cf2, k=100).as_decimal()
Decimal('0.5024390243902439024390243902439024390243902439024390243902439024390243902439024390243902439024390244')

and right-mediants:

>>> cf1 = ContinuedFraction('1/2')
>>> cf2 = ContinuedFraction(3, 5)
# The default `k = 1` gives you the common, simple mediant of the two rationals
>>> cf1.right_mediant(c2)
ContinuedFraction(4, 7)
>>> cf1.right_mediant(cf2, k=2)
ContinuedFraction(7, 12)
>>> cf1.right_mediant(cf2, k=100)
ContinuedFraction(301, 502)
>>> cf1.right_mediant(cf2, k=100).as_decimal()
Decimal('0.5996015936254980079681274900')

As \(k \longrightarrow \infty\) the left- and right-mediants form different, strictly monotonic, sequences converging to opposite limits: the left-mediants form a strictly decreasing sequence lower-bounded by \(\frac{a}{b}\):

\[\frac{a}{b} < \cdots < \frac{3a + c}{3b + d} < \frac{2a + c}{2b + d} < \frac{a + c}{b + d} < \frac{c}{d}\]

thus converging to \(\frac{a}{b}\):

\[\lim_{k \to \infty} \frac{ka + c}{kb + d} = \lim_{k \to \infty} \frac{a + \frac{c}{k}}{b + \frac{d}{k}} = \frac{a}{b}\]

while the right-mediants form a strictly increasing sequence upper-bounded by \(\frac{c}{d}\):

\[\frac{a}{b} < \frac{a + c}{b + d} < \frac{a + 2c}{b + 2d} < \frac{a + 3c}{b + 3d} < \cdots < \frac{c}{d}\]

thus converging to \(\frac{c}{d}\):

\[\lim_{k \to \infty} \frac{a + kc}{b + kd} = \lim_{k \to \infty} \frac{\frac{a}{k} + c}{\frac{b}{k} + d} = \frac{c}{d}\]

We can see with the ContinuedFraction(1, 2) and ContinuedFraction(3, 5) instances used in the examples above, starting with the left-mediants:

>>> cf1 = ContinuedFraction(1, 2)
>>> cf2 = ContinuedFraction(3, 5)
>>> cf1.left_mediant(cf2)
ContinuedFraction(4, 7)
>>> cf1.left_mediant(cf2).as_decimal()
Decimal('0.5714285714285714285714285714')
>>> cf1.left_mediant(cf2, k=10).as_decimal()
Decimal('0.52')
>>> cf1.left_mediant(cf2, k=100).as_decimal()
Decimal('0.5024390243902439024390243902439024390243902439024390243902439024390243902439024390243902439024390244')
>>> cf1.left_mediant(cf2, k=10 ** 6)
ContinuedFraction(1000003, 2000005)
>>> cf1.left_mediant(cf2, k=10 ** 6).as_decimal()
Decimal('0.5000002499993750015624960938')

And then the right-mediants:

>>> cf1 = ContinuedFraction(1, 2)
>>> cf2 = ContinuedFraction(3, 5)
>>> cf1.right_mediant(cf2).as_decimal()
Decimal('0.5714285714285714285714285714')
>>> cf1.right_mediant(cf2, k=10).as_decimal()
Decimal('0.5961538461538461538461538462')
>>> cf1.right_mediant(cf2, k=100).as_decimal()
Decimal('0.5996015936254980079681274900')
>>> cf1.right_mediant(cf2, k=10 ** 6)
ContinuedFraction(3000001, 5000002)
>>> cf1.right_mediant(cf2, k=10 ** 6).as_decimal()
Decimal('0.5999999600000159999936000026')

References#

[1] Baker, Alan. A concise introduction to the theory of numbers. Cambridge: Cambridge Univ. Pr., 2002.

[2] Khinchin, A. Ya. Continued Fractions. Dover Publications, 1997.

[3] Wikipedia. “Continued Fraction”. https://en.wikipedia.org/wiki/Continued_fraction. Accessed 19 February 2024.

[4] Wikipedia. “Farey sequence”. https://en.wikipedia.org/wiki/Farey_sequence. Accessed 10 March 2024.

[5] Wikipedia. “Mediant (mathematics)”. https://en.wikipedia.org/wiki/Mediant_(mathematics). Accessed 23 February 2024.

[6] Wikipedia. “Stern-Brocot Tree”. https://en.wikipedia.org/wiki/Stern%E2%80%93Brocot_tree. Accessed 23 February 2024.

On this page
Show Source